Fermat's method of calculus
I've attached my question as a file and here is the resource I was looking at https://cedar.wwu.edu/cgi/viewcontent.cgi?article=1012&context=wwu_honors
 Markgvanzalk
Markgvanzalk
96
Answer
Answers can only be viewed under the following conditions:
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
 Mathe
Mathe
3.7K
-
can you explain further the last part you wrote?
-
In essence, this procedure allows to find the x-axis cross value as a limit operation. When we replace T(x+epsilon) by f(x+epsilon) we are thinking of a sufficiently small epsilon for this to make sense. This is a limit operation t that is quite literally based on Taylor first order approximation.
-
I added another explanation.
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
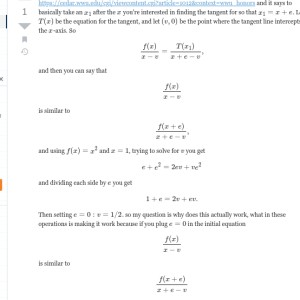

what is the question?
you are asking why does this actually work even after answering the same. But you are also sayng you wont get anywhere
Your question is very vague. Please clarify.
my question basically is why does this method work to give you a tangent line? specifically the steps where you divide by e and then plug 0 in for e