Sum of infinite series
If you noticed, without the summation notation, it is the present value money formula with finite time period.
PV - present value
FV - future value
i - interest rate
n - number of years
PV = FV/(1+i)^n
The present value money formula with indefinite time period is
PV = D / i
D - dividend (which is FV every year)
I'm curious if the infinite summation of FV/(1+i)^n (see the picture attached) is D / i.
Step by step process and explanation appreciated.
Answer
Answers can only be viewed under the following conditions:
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
Erdos
4.8K
-
Please leave a comment if you need any clarifications.
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- answered
- 1380 views
- $4.00
Related Questions
- Solve summation problem: $\sum_{k=1}^{n} \tfrac{2k+1}{k^{2}(k+1)^2 } $
- Taylor polynomial
- Why does $ \sum\limits_{n=1}^{\infty } 2^{2n} \times \frac{(n!)^2}{n(2n+1)(2n)!} =2 $ ?
- Probe the following sequences is null
- Is $\sum_{i=1}^{\infty}\arctan (\frac{n+1}{n^2+5})$ convergent or divergent?
- Convergence of $\sum\limits_{n=1}^{\infty}(-1)^n\frac{n+2}{n^2+n+1}$
- Arithmetic Sequences Help
- Recursive square root sequence
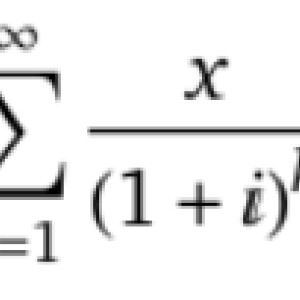
Your question is vague. Do you want to compute the sum in the attached picture? What is x?