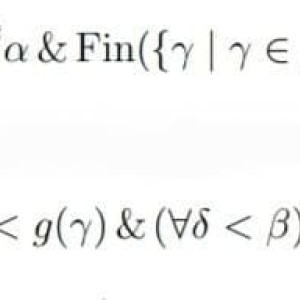Prove a set is well-ordered
Let $FS(α, β) ⇋ { f | f : β->α & Fin( {γ | γ ∈ β & not( f(γ) = 0 ) })}$ for all ordinals α, β,
where Fin(A) means the set A is finite.
We define a relation ≺ on FS: $f ≺ g ←→ (∃γ < β)( f(γ) < g(γ) & (∀δ < β)( γ < δ ⇒ f(δ) = g(δ)))$.
How to prove that (FS, ⪯) is well-ordered?
Answer
Answers can only be viewed under the following conditions:
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
1.7K
-
On the second step of the induction you mean FS(L, B) = FS(L, Г) x L are isomorphic right?
-
Yes, exactly.
The answer is accepted.
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.