Closest Points on Two Lines: How to use algebra on equations to isolate unknowns?
I am studying linear algebra in my spare time, and reading a textbook.
It has been a long time since I've had to do basic algebra, so I am completely lost as to how to reformulate / use substitition to isolate variables and solve for these equations.
I am looking for someone to break down step-by-step how I can go from one set of equations to the rearranged version of equations. It is really important that no step, no matter how small of an algebriac step, is missed in your explanation, because I want to make sure I really understand how to break it down.
Here is the original set of equations:
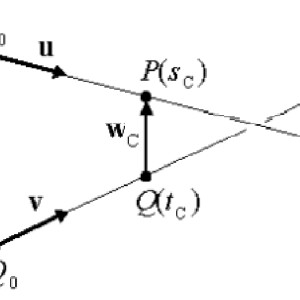
u and v are vectors.
Sc and Tc are scalars that we the unknowns we are trying to solve for.
W0 is a vector: W0 = P0 - Q0, where Q0 is the origin of line 2, P0 is the origin of line 1.
(u dot u) * Sc - (u dot v) * Tc = - u dot W0
(v dot u) * Sc - (v dot v) * Tc = - v dot W0
The textbook then jumps into the following explanation, without breaking down the steps of how to get there:
a = u dot u
b = u dot v
c = v dot v
d = u dot W0
e = v dot W0
We can solve for Sc and Tc as:
Sc = (b*e - c*d) / (a*c - b*b)
Tc = (a*e - b*d) / (a*c - b*b)
From what I have gathered, in the first set of equations we are isolating Sc to one side in one equation, Tc to one side in the other equation, and then substititing that into each others equations so we reduce from two unknowns to one unknown in each equation.
But I am struggling with the rearranging itself and then reducing it down into variables a-e and then rearranging those to end up with the final two equations.
Can anyone help? Thank you!
Eric
Answer
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
2 Attachments
Erdos
-
I appreciate the answer, but your explanation is a regurgitation of the problem that I am having an issue with. I do not know how to solve that last step via a system of equations approach. I am looking for someone to break down step-by-step that process of turning those last two equations into this: a = u dot u b = u dot v c = v dot v d = u dot W0 e = v dot W0 We can solve for Sc and Tc as: Sc = (b*e - c*d) / (a*c - b*b) Tc = (a*e - b*d) / (a*c - b*b)
-
This is my first time using this platform and I want to give you an opportunity to revise your answer before I dispute it. I am worried if I dispute it it will disqualify you from editing your question. So I will refrain from disputing for a few hours.
-
And to be clear, as I mentioned in the original post, I want a step-by-step (literally STEP by STEP) breakdown of how I go from this: (u dot u) * Sc - (u dot v) * Tc = - u dot W0 (v dot u) * Sc - (v dot v) * Tc = - v dot W0 To this: a = u dot u b = u dot v c = v dot v d = u dot W0 e = v dot W0 Sc = (b*e - c*d) / (a*c - b*b) Tc = (a*e - b*d) / (a*c - b*b)
-
I will add the details of how the system is solved soon.
-
See the second file I uploaded for the details of how the system is solved.
-
Your question took me over 30 minutes to answer. Consider offering higher amounts for your future posts, otherwise users here may not have enough incentive to accept.
-
Hey Philip, thanks a bunch for elaborating on your original answer, this is exactly what I was looking for! I apologize if I had offered too low of a bounty, as mentioned before this was my first time on the platform and I didn't have a feel for what was a fair price. I agree that 30 minutes is a long time for $5, so in the future I will try to scale it more appropriately. In the meantime, if you have Venmo or Paypal, feel free to share that here and I will provide a tip.
-
You're welcome Eric. No need for Venmo or PayPal. I am glad I was able to help. Please recommend the website for friends and family, if you had a good experience.
- answered
- 725 views
- $5.00
Related Questions
- Motorcycle Valve Clearance Calculation and Spacer Size Word Problem
- Use first set of data to derive a second set
- Does $\lim_{n \rightarrow \infty} \frac{2^{n^2}}{n!}$ exist?
- Algebra problem
- Zariski Topology and Regular Functions on Algebraic Varieties in Affine Space
- I really can't figure out equations with a power of 2 in it, please solve these and explain every step as if I was a baby.
- There are a total of 95 coins, quarters and dimes, and the total is $15.35. How many dimes are there ?
- Algebraic and Graphical Modelling Question
"Sc and Tc are scalars that we the unknowns we are trying to solve for." should be: "Sc and Tc are scalars that are the unknowns we are trying to solve for."