Applications of Integration [Calculus 1 and 2]


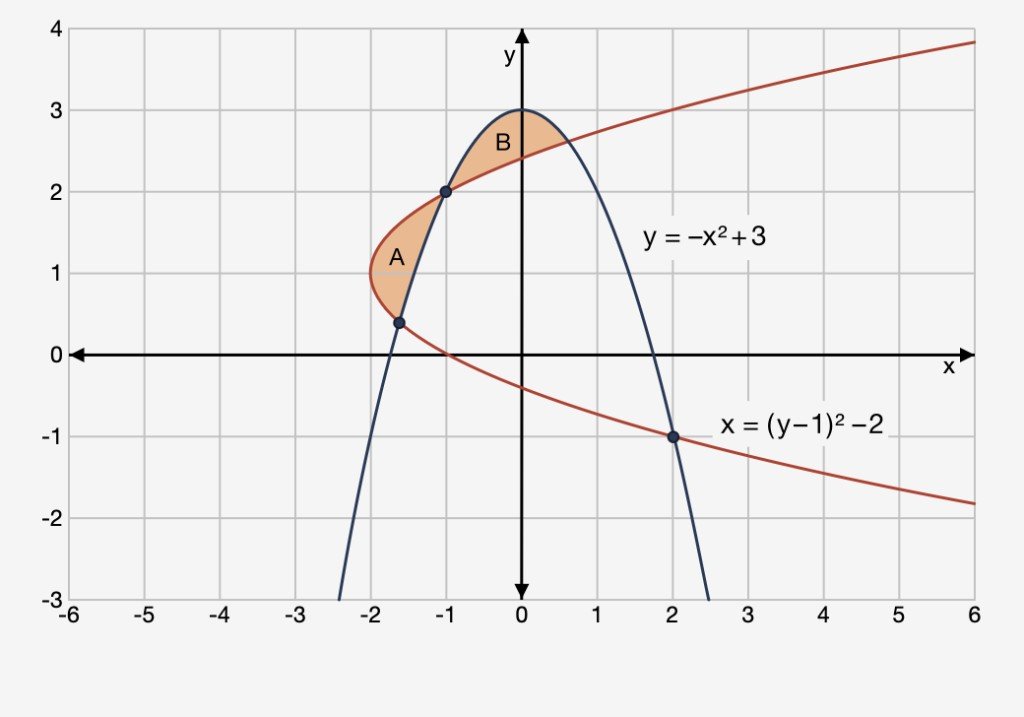
For the regions A and B shown in the graph:

Part A: Discuss the limits of integration. (3 points)

Part B: Set up an integral expression that represents the total area. (4 points)

Part C: Calculate the total area. (3 points)

Calculus Integrals
Nicolas Santana Nicolas Santana
300
Matchmaticians Applications of Integration [Calculus 1 and 2] File #1 File #1 (png)
Report

Answer

Answers can only be viewed under the following conditions:
  1. The questioner was satisfied with and accepted the answer, or
  2. The answer was evaluated as being 100% correct by the judge.
View the answer

1 Attachment

Kav10 Kav10
2.1K
  • Nicolas Santana Nicolas Santana
    0

    What are the Limits of integration? So Interval Notation?

    • Kav10 Kav10
      +1

      The limits of integration are written in the seventh line. 2 and (3-sqrt(5))/2.

    • Kav10 Kav10
      +1

      Does that make sense?

  • Nicolas Santana Nicolas Santana
    0

    But they should be this intervals of region A and B so: Region A: From -2 to -1 Region B: From -1 to 0.6 (which is the square root used)

    • Kav10 Kav10
      0

      No, when integral is dy, the interval should be from y axis, when it is dx, the interval should be from x axis. See the solution where it uses the y limits for the integral …dy and x limits for integral …dx. Does that make sense now?

  • Nicolas Santana Nicolas Santana
    0

    Yes, so you used Horizontal slices

The answer is accepted.
Join Matchmaticians Affiliate Marketing Program to earn up to a 50% commission on every question that your affiliated users ask or answer.