I need help solving a graph theory problem that has a strict set of unique rules
I need help developing the pseudocode of an algorithm that can solve the following problem:
Given a simple undirected graph of n positively weighted nodes with unweighted edges, return a result containing sets of nodes found under the following rules:
1. Sets must contain exactly two pairs of two nodes, where the nodes within a pair are connected by an edge
2. The result contains each node at most once
3. As many sets as possible are in the result. Specifically, (n - (n % 4)) / 4 sets are in the result
4. The result has the smallest possible result weight. The result weight is calculated as follows: Imagine a graph with eight nodes, named A, B, C, and so on until H. Pairs of nodes will have a pair weight which for nodes A and B with weights Aw and Bw, is Aw + Bw. Sets will have a set weight which for pairs AB and CD with pair weights ABw and CDw, is | ABw - CDw |. The result will have a result weight which for sets ABCD and EFGH with set weights ABCDw and EFGHw, is ABCDw + EFGHw
If any of the rules cannot be met, then return a result with zero sets
Maddog
10
Join Matchmaticians Affiliate Marketing
Program to earn up to a 50% commission on every question that your affiliated users ask or answer.
- answered
- 889 views
- $30.00
Related Questions
- Determine the number of perfect pairings in a complete bipartite graph Kn,n, in which n disjoint edges are removed.
- Determine the Closed Form of a Recurrance Relation
- Characterizing the Infinitely Visited Intersections in a Ride-Forever Path on a Directed Graph
- Graph Theory Question
- Discrete Math Question
- Prove that in 2-edge-connected graph, each vertex lies on a cycle.
- Clock Problem
I would ask to rewrite the question because it's difficult to read.
The bounty is low for the level of the question and the time one needs to spend to write a good solution.
A few clarifications: Must the edge between pairs exist in the underlying graph? Do we ignore the remainder that cannot be partitioned into a subgraph of 4? Finally, and you can ignore this if you'd like, but what's the inspiration for this problem? Knowing that can help motivate a model.
Thank you for the feedback Mathe and Daniel90. Larrybo, here are the answers to your questions: 1. Yes an edge must exist between nodes for them to be a pair per rule 1. 2. Yes you may ignore all nodes left over after the maximum number of sets are in the result as defined in rule 3 3. I will unfortunately refrain from answering the inspiration for the problem statement
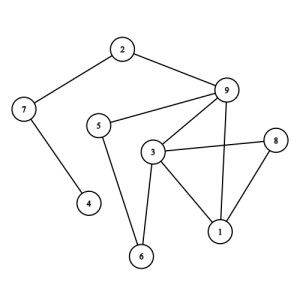
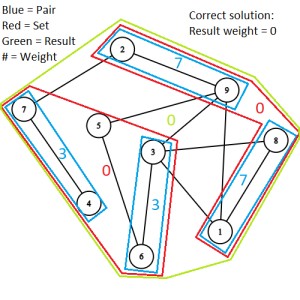
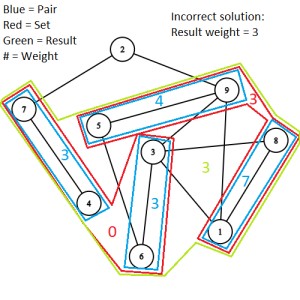
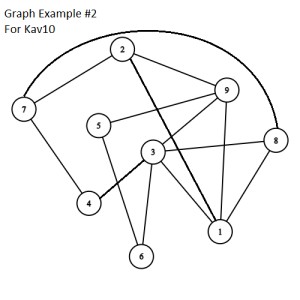
I have added pictures to this problem to help with visualizing it. File 1 is an example graph with n = 9. File 2 is an example of a correct solution for the graph. We know this is a correct solution because the result weight is 0, which is as small as possible. That's not to say for some graphs the smallest result weight may be above 0 or there may be other results with a result weight of 0. File 3 is a duplicate of file 2, my mistake. File 4 is an example of an incorrect solution for the graph.