Prove that $ \sum_{k=1}^{\infty} (-1)^k q^{k^2} \geq \frac{2}{\pi}\ \sum_{k=1}^{\infty} \frac{(-1)^k}{2k-1}{q}^{\frac{ (2k-1)^2}{4}}  $ for $0<q<1$ (updated bounty)

With the simplifications I suggested, in particular writing the left hand side (LHS) as 
$f(q) = \sum_{k\ge1} (-1)^k q^{k^2}$
and similar for the R.H.S. of the inequality,
$g(q) = \frac2\pi\sum_{k\ge1}\frac{(-1)^k}{2k-1}\,q^{(k-1/2)^2}$, 
the question amounts to show that the function
$h(q) := f(q) - g(q)$
is nonnegative over the open interval (0, 1).
(As we shall see, this function admits the limit zero at both endpoints of that interval and could thus be extended by continuity to the closed interval.)

For a physicist or engineer it could be proof enough to plot that function on the interval (0,1) ; that plot looks as follows :

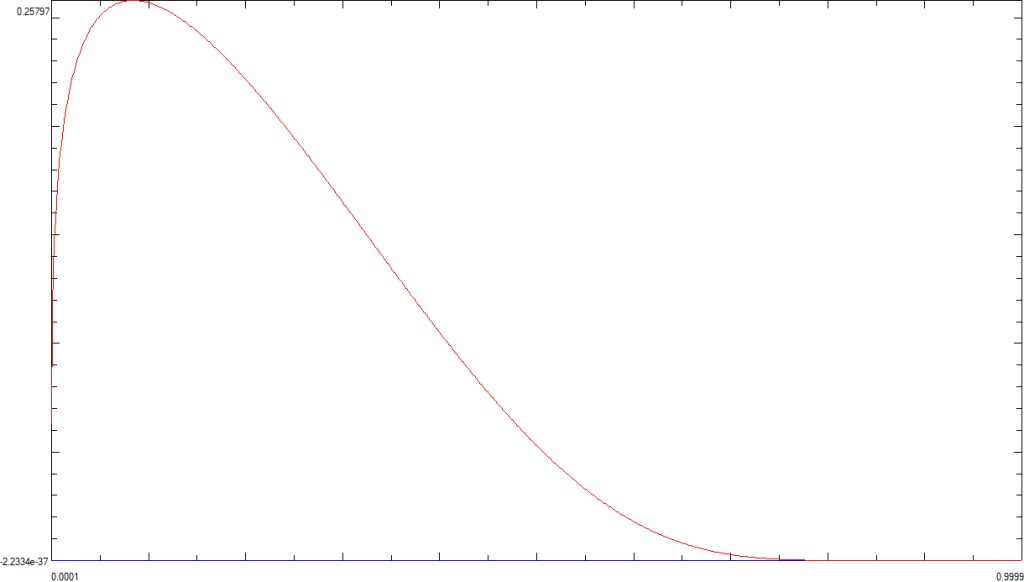
Here is code that can be pasted into the free PARI/GP online interpreter at http://pari.math.u-bordeaux.fr/gp.html to reproduce this plot or a "zoom" on any subinterval $[a,b] \subset (0, 1)$:

{ ( f(q) = sumalt(k=1,(-q)^k^2) );
( g(q) = sumalt(k=1, (-1)^k/(2*k-1)*q^(k-.5)^2)*2/Pi );
ploth( q=1e-5, 1-1e-5, f(q)-g(q)) }

The plot shows (upon "zooming in" where necessary, e.g., q=0.08, 0.09) that:

(1) $h(q) \to 0^+$ as $q\to 0^+$,

(2) $h(q)$ is increasing on some interval $(0,m)$, $0 < m < 1$,

(3) $h(q)$ reaches its maximum $ M = h(m) \approx 0.257972 $ at $ m \approx  0.0840863 $,

(4) $h(q)$ decreases on $(m, 1)$,

(5) $h(q) \to 0^+$ as $q\to 1^-$ (i.e., as q approaches 1 from the left),

(6) the maximum $M=h(m)$ is the only local extremum, and we have the two global minima $h=0$ at the endpoints $q=0$ and $q=1$, assuming that we extend the function by continuity to the closed interval [0, 1].

Here, (2) is a consequence from (1) (with so far unspecified $m$), and similarly (4) is a consequence from (5) if we take $m$ again unspecified. The nontrivial part of these two is that the $m$ in (2) and the one in (4) are both equal to that given in (3), i.e., the unique point where $h$ takes a local extrema which is a maximum.

The result of (3) is easily proved numerically. We will try to address further below the much more challenging question to get some formula or estimate for the numerical value of $m$.

Although a numerical approach is acceptable and often the only solution if analytical results are infeasible, this is not very satisfying for a mathematician, so I will try to establish some more analytical / algebraical results.

To that end, let us group together the terms from the two sums, and write

$ h(q) = \sum_{k\ge1} (-1)^k \, [q^{k^2} - \frac{2/\pi}{2k-1}\, q^{(k-1/2)^2}]$.    (7)

=== Behaviour near zero ===

To get a better idea, let us write out the sum of the first terms with $1 \le k\le 3$:

$ h(q) = -q + q^4 - q^9 + \frac2\pi \, ( q^{1/4} - q^{9/4} +  q^{25/4}) + O(q^{49/4})$  ( as $q\to 0^+$ ).     (8)

Obviously, for very small $q\to 0^+$, all terms are negligible w.r.t. the first term ($k=1$) in $g(q)$,

$h(q) \sim \frac 2\pi \, q^{1/4} ~$  as  $~ q\to 0^+$.

(We can also double-check this result numerically by computing $h(10^{-4}) \approx 0.06356 \approx \frac2\pi\times 0.09984 \approx \frac2\pi \,10^{-1}$.)

We also note that the exponents grow very fast (namely, like $k^2$), which means that for small $q$, the terms with larger $k$ are quickly negligible: for example, 

$h(0.1) = - 0.1 + 10^{-4} - 10^{-9} +- … +\frac2\pi \,( 10^{-1/4} - 10^{-2.25} + 10^{-6.25} -+...)$
$\approx \frac2\pi \,10^{-1/4} - 0.1 = 0.2579976 $ within less than 0.01, considering just two terms.

This is actually a quite good approximation of the value of the maximum $M \approx 0.25797$ which we have numerically located at $ q = m \approx 0.084 $.
This suggests that over the interval (0, 0.1) and presumably somewhere beyond, the function 

$h_1(q) = \frac2\pi \,q^{1/4} - q ~$  is a quite acceptable approximation of our target function $h(q)$. 

This function has its maximum where its derivative,  $h_1'(q) = \frac1{2\pi}\,q^{-3/4} - 1$, has its zero, which is at $q_1 = (2\pi)^{-3/4} \approx 0.86$. This is a first formula for an approximation of the value $m$ that appears in properties (2), (3) and (4).

We get an even better approximation if we include one or two more terms, viz

$h_2(q) = \frac2\pi \,(q^{1/4} - \frac13 \,q^{9/4}) - q ~$  or  $~ h_3(q) = \frac2\pi \,(q^{1/4} - \frac13 \,q^{9/4}) - q + q^4 $.

We find $h_2'(q) = \frac1{2\pi} (q^{-3/4} - 3\,q^{5/4}) - 1$ which has its zero at $q_2  \approx 0.0838341$, an even better approximation of the value of $m$. (There is no exact expression for this value or the subsequent approximation below: they are roots of polynomials of degree 8 and higher.)

Similarly, $~ h_3'(q) = \frac1{2\pi} (q^{-3/4} - 3\,q^{5/4}) - 1 + 4\,q^3 ~$ has its zero at $~q_3 = 0.0840860756…~$, which is an extremely good approximation of the point $m$ where $h$ takes its maximum.

[PARI code: solve(q=0.05,0.1, (q^(-3/4) - 3*q^(5/4))/2/Pi - 1 + 4*q^3) ]

=== Behaviour in $(m,1)$ ===

The function $h_3$ is a quite good approximation of $h(q)$ way beyond the maximum at $m\approx 0.1$.
It is well known that the error made by truncating an alternating series $S = \sum (-1)^k a_k$ ($a_k$ decreasing to 0) at some index $k$, is majorated by the next term, $|S - S_k| \le |a_{k+1}|$ (where $S_k$ is the partial sum up to $k$).

For example, at $q = 0.5$, the sum of all terms with $k\ge3$ in $f$ and $g$, respectively, are smaller than $0.5^{9} = \frac1{512}$ and $\frac2{5\pi}\cdot 0.5^{25/4}\sim 0.00167$, respectively (in absolute value).
(The actual error is significantly smaller, because these two major contributions to the error are of comparable size but opposite sign and so they cancel out each other to a large extend.)

We find that up to at least $q = 0.6$, the function $h_3(q)$ is larger than the sum of the two "error terms" $q^9+\frac2{5\pi}\,q^{25/4}$, which proves that the function $h$ is positive up to there at least.

In the available time, I did not find a satisfying way to prove analytically that $h$ remains positive as $q\to 1^+$, so I have nothing better to offer than a numerical proof that this is the case, considering the function on several intervals from 0.6 to 1.0.

As $q$ grows from 0.6 to 1, I will use that the infinite sum is strictly positive whenever we have some $n$ such that the partial sum
$S_n :=\sum_{k=1}^n(-1)^k(a_k-b_k) > E_{n+1}$ ,
where $E_n := |a_n| + |b_n|$, $a_k=q^{k^2}$, and $b_k=q^{(k-1/2)^2}/(\pi(k-1/2))$.

We will increase q in sufficiently small steps so that we can have confidence that the behaviour in subsequent values is "continuous". (Of course one could check further intermediate values.)

Here's the list of terms (k, $a_k$, $b_k$, $S_k$) for $q = 0.6$:

k = 1: -0.6                +0.560297     -0.0397035
k = 2: +0.1296         -0.0672356    +0.0226609
k = 3: -0.0100777    +0.00522824  +0.0178115
k = 4: +0.0002821   -0.000174235 +0.0179194
k = 5: -2.84303e-6   +2.27615e-6  +0.0179188
k = 6: +1.03144e-8  -1.12606e-8   +0.0179188

Here, as we said, the terms for k=1 and 2 sum up to $S_2 \approx 0.02266$, while those for k=3 sum up to $E_3=0.015$ in absolute value, which proves that the function is strictly positive near that point.
(Of course this remains true if we truncate only at k = 3, where the partial sum is 30 times larger than the sum of absolute values of terms for k = 4.)

List of terms (k, $a_k$, $b_k$, $S_k$) for q = 0.7:

k = 1: -0.7                 +0.582311       -0.117689
k = 2: +0.2401           -0.0951107      +0.0272998
k = 3: -0.0403536      +0.0137016      +0.000647841
k = 4: +0.00332329    -0.00115142    +0.00281972
k = 5: -0.000134107   +5.16265e-05  +0.00273724
k = 6: +2.65173e-06   -1.19317e-06  +0.00273869
k = 7: -2.56924e-08   +1.39743e-08  +0.00273868
k = 8: +1.21976e-10   -8.21398e-11  +0.00273868

Here we have to truncate at k = 4 (or later), where the partial sum is $S_4 \approx$ 2.8e-3,
and the "error terms" are $E_5$ = 1.3e-4 + 5e-5 = 1.8e-4.

List of terms (k, $a_k$, $b_k$, $S_k$) for q = 0.8:

k = 1: -0.8               +0.602078      -0.197922
k = 2: +0.4096         -0.128443      +0.0832345
k = 3: -0.134218       +0.0315662    -0.019417
k = 4: +0.0281475    -0.00591064   +0.00281989
k = 5: -0.00377789   +0.000771276 -0.000186727
k = 6: +0.000324519 -6.77578e-05 +7.00336e-05
k = 7: -1.78406e-05  +3.93993e-06 +5.61329e-05
k = 8: +6.2771e-07   -1.50176e-07  +5.66104e-05

Here we must truncate not earlier than k = 6 to have a partial sum $S_6 \approx$ 7e-5 
(significantly) larger than the sum of error terms, $E_7 \approx$ 1.8e-5 + 3.9e-6 = 2.8e-5.


Terms (k, $a_k$, $b_k$, $S_k$) for q = 0.9:

k = 1:   -0.9             +0.62007           -0.27993
k = 2:  +0.6561        -0.167419          +0.208751
k = 3:  -0.38742       +0.0659061        -0.112763
k = 4:  +0.185302     -0.025018          +0.0475208
k = 5:  -0.0717898     +0.00837623     -0.0158928
k = 6:  +0.0225284     -0.00238959     +0.00424601
k = 7:  -0.00572642    +0.000571061   -0.000909341
k = 8:  +0.00117902   -0.000113222    +0.000156456
k = 9:  -0.000196627  +1.8512e-05     -2.16593e-05
k = 10: +2.65614e-5  -2.48607e-06     +2.41599e-06
k = 11: -2.90632e-6   +2.73462e-07    -2.16872e-07
k = 12: +2.57585e-7  -2.45881e-08     +1.61249e-08
k = 13: -1.8492e-8     +1.8044e-09     -5.62678e-10
k = 14: +1.07531e-9  -1.07948e-10     +4.0468e-10
k = 15: -5.06483e-11  +5.25981e-12   +3.59291e-10

Here we cannot truncate before k=14 if we want to use the same criterion.


Terms (k, $a_k$, $b_k$, $S_k$) for q = 0.95:
k = 1:   -0.95          +0.628508    -0.321492
k = 2:  +0.814506   -0.189076     +0.303938
k = 3:  -0.630249    +0.0924023   -0.233909
k = 4:  +0.440127   -0.0485173    +0.157701
k = 5:  -0.27739      +0.0250346  -0.0946544
(...)
k = 25: -1.194685e-14    +5.524311e-16   -7.806533e-16
k = 26: +8.732874e-16    -4.083986e-17   +5.179421e-17
k = 27: -5.761138e-17    +2.729016e-18   -3.088155e-18
k = 28: +3.430098e-18    -1.648139e-19   +1.771297e-19
k = 29: -1.843113e-19    +8.995052e-21   +1.813372e-21
k = 30: +8.938091e-21    -4.436042e-22   +1.030786e-20
k = 31: -3.911872e-22    +1.976670e-23   +9.936438e-21
k = 32: +1.545154e-23    -7.957688e-25   +9.951094e-21

Here we have $S(k) > E(k+1)$ only for $k$ ≥ 30.
(PARI code to produce that table for any q is given in the Appendix.
Note that Python with standard precision of 16 digits is no more adequate at this point.)

For $q=0.98$, we find that we can truncate only at $k = 76$, even at $k = 75$ we still have one last negative partial sum:
(...)
k = 74: +8.994779 e-49   -1.728344 e-50   +4.161561 e-50
k = 75: -4.432776 e-50   +8.574730 e-52   -1.854677 e-51
k = 76: +2.098037 e-51  -4.086403 e-53    +2.024966 e-52
k = 77: -9.536802 e-53   +1.870640 e-54   +1.089992 e-52

(Obviously a precision of at least 55 digits is required to get significant results in this computation.)

In the appendix I give a program ("tab(q,...)") for computing this table for any desired value of $q$.

It would be desirable to have an expression for the rank from which on we have this property, but I found some flaws in previous attempts and finally cannot provide such an expression within the alloted time.
Several other attemps (series in $q = 1-\varepsilon$ or $q = e^{-\varepsilon}$, ...) also did not bring more enlightment so far.

===============================
=====     Appendix :    =====

=== Further sample PARI code and additional remarks and formulae ===

(f(1e-4)-g(1e-4))*Pi/2  \\ gives: 0.0998429200... , illustrating lim (f-g) ~ $\frac \pi2 \sqrt q $ near $q=0$.

f(.999)-g(.999)  \\ gives: 1.103774179 E-26

/* illustrating $ \lim f = \lim g = - 0.5$ as $q\to 1$ : */

f(0.99) \\ gives:  -0.499999999999

g(0.99) \\ gives: -0.5000000000  

Side note/insider joke: Euler would certainly have been happy that we get $\lim_{q\to1-} f(q) = -1 +1 -1 +1 -+ ... = -1/2 $ ...!
(Of course the middle expression is not to be taken serious!
But we know that the series is well convergent since it is an alternating series: signs alternate and the absolute values go to zero as increasingly high powers of a number less than 1.
The series is even absolutely convergent since, taking absolute values (which gives $f(-q)$), we have something much smaller than the geometric series $\sum _{n\ge0} q^n = \frac1{1-q} <\infty$, since only the terms with square indices $n = 1, 4, 9, 25, ...$ appear in our sum $f(-q)$.)


PARI code to produce the table (k, ak, bk, Sk):

/* Use e.g., tab(0.9). The second, optional argument is the upper limit of rows to display. By default this is set to 50. If more rows are required / desired, use e.g. tab(0.98, 99).
Also, use " default(realprecision, N) " (or the shortcut \p N) to increase the precision to N digits if the default precision (N=39 on 64 machines) is no more sufficient: 10^(-N) should always be significantly smaller than all of the terms in the last displayed row.
*/

tab(q,LIM=50)={my(S,T); for(k=1,LIM, my(A=(-q)^k^2, B=-(-1)^k*q^((k-.5)^2)/Pi/(k-1/2));
if(abs(A)+abs(B) < S, T++, T=0);
printf("k = %d:\t %+7.7g \t %+7.7g \t %+7.7g\n", k, A, B, S += A+B);
T>1 && break )}


It may also be interesting to rewrite, using $(k-1/2)^2 = k^2-k-1/4$:

$ h(q) = \sum_{k\ge1} (-1)^k \, [q^{k+1/4} - \frac{2/\pi}{2k-1}]\, q^{(k-1/2)^2}]$.   
(...)