Gear - Wing Spar Linkage
Hi All,
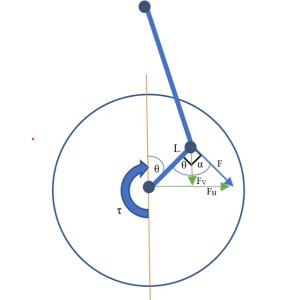
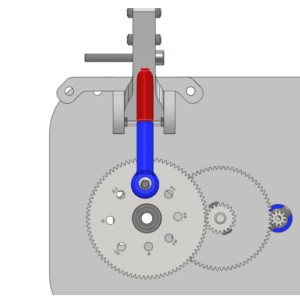
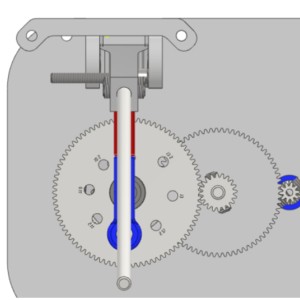
I am building a robotoc bird and have drive mechanism with a gear that has a linkage attached to it at some distance (L) like in the picture (#2 and #3). I am trying to find the vertical component of force given a torque for each cycling period.
I have derived the free body diagram (#3) with the following equation to get the vertical component.
F_v = F*cos(90-theta)
Theoretically this makes sense but intuitively thinking about it, at 90 deg, FV should equal F as the force from the gear acts tangentially to the moment arm L
Any help would be greatly appreciated, maybe I need to draw a simpler free body diagram, been staring at this for hours and can't figure out what I am missing.
Answer
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
Savionf
-
Let me know if you have any questions.
-
Hi Savionf Thank you for taking the time to answer. Would you say this free body diagram is the best representation of the system. I am skeptical that this representation actually represent the forces acting at point at which the linkage is attached to the wing spar. (Upper most point on (#1) but rather that it is representative Soley of the vertical component of force at the gear. Does this make sense??
-
It is hard to answer your questions in general as it could depend on what you really want to do, but the formula you have for F_v seems reasonable, both mathematically and intuitively. F_v is the force which makes the gears to rotate. As you can see, the force results in minimum rotation when theta=0 and maximum rotation when theta=90 degrees.
-
- answered
- 1901 views
- $10.00
Related Questions
- Find the real solution of the equation $x^{2}-10=x \sin{x}$.
- Trigonometry Word Problems
- Evaluate $\int \frac{x^5}{\sqrt{x^2+2}}dx$
- A trigonometry question
- Solving for two unknown angles, from two equations.
- Create a Rotation Matrix for 3 point x,y vectors
- Somewhat simple trig question
- Simplify this expression
