Probability - what is the probability that a given tire length will lie in a lenght of interest
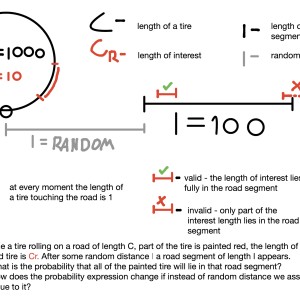
Walking across a street and lookign at tires I've had a thought. If a car is rolling on a road starting at point O, at each time some area of a tire is touching the road, what if after some random distance L there are 2 points - A and B, the distance from A to B is 100cm.
A tire of that car has a length of 1000cm, of that 1000cm, 10cm is painted red - R.
What would be the probablity that all of the painted area R would be inside points A and B. The area R would need to lie fully inside A & B, it can't start in outside of AB and end in AB or start in AB and end outside of AB - only in between AB.
How the probability expression would change if instead of random distance L we would assign a distance from point O to A. My first thought is that it would not change as there is another random factor - what is the starting position of a tire ( where the area R is from the starting point O ).
I've added an image drawing this question for easier visualization.
 Jonisas
Jonisas
Answer
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
 Larrybo
Larrybo
-
Thank you for your answer, shouldn't in the very top instead of R > T be L > T?
-
So for example, I have a tire T with circumference of 1000, painted part R is 10, the length of a road L is 100. My intuition would suggest that the probability of R being inside of L is very low because it is a small part of the tire, in othercase if L >= T+R the probability is 1. If I calculate the probability using your formula I get that the probability is 90%, which is not what I expect, unless I understood it wrong.
-
Oh! I think I confused the problem a bit. I thought it was a one meter tire on a one-kilometer road, but you're talking about a 10 meter tire (monster truck!) running on a one meter road with a 10 cm painted part. This answer was taken assuming the road was longer than the tire length, but re-reading your question I now see that is not the case. I will re-write the answer tomorrow.
- answered
- 1576 views
- $10.00
Related Questions
- Assess team win rate by combining individual win rates?
- What are the odds of at least k same outcomes in n independent trials, each with x equally likely outcomes?
- Using probability to calculate expected time a task would take with "bad" luck
- Suppose that X is a random variable uniform in (0, 1), and define $M = 2 \max\{X, 1− X\} − 1$. Determine the distribution function of M.
- Probability
- Differently loaded dices in repeated runs
- Probability and Statistics Question help please
- Find the maximum likelihood estimate

$2.90? Surely that was a typo
I thought this is an easy question for someone who is working with probability and wouldn't take more than 5 minutes. I've increased my bounty.