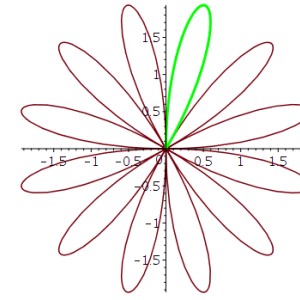
Rose curve
In the figure below you will see a "flower" with a green leaf limited by a closed simple curve, calculate the area of the curve:
$$r(t)=(cos(5t)-cos(7t),sin(5t)+sin(7t)),$$
for $t\in (0,\pi/6)$.
You can use the trigonometric formula : $\cos u \cos v= 1/2\cos(u+v)+1/2\cos(u-v)$.
Asara
Answer
Your curve is given by $r(t) = (x(t),\ y(t))$,
where
- $\red{x(t) = cos(5t) - cos(7t)}$
- $ \blue{y(t)= sin(5t) + sin(7t)}$
The area of the "petal" of interest will be given by
$$A = \int_{\pi/6}^0 \red{x(t)}\blue{ y'(t)} dt $$
Remark: The intervals of the integral is define by the orientation of the curve.
Then, we need to compute $\blue{y'(t)}$,
$$\blue{y'(t) = 5 cos(5 t) + 7 cos(7 t) }$$,
so that the integral become,
$$A = \int_{\pi/6}^0 \red{\left( cos(5t) - cos(7t) \right)} \cdot \blue{\left(5 cos(5 t) + 7 cos(7 t)\right)}dt $$
$$\Rightarrow A = -t+\frac{1}{2} \sin (2 t)+\frac{1}{4} \sin (10 t)+\frac{1}{12} \sin (12 t)-\frac{1}{4} \sin (14 t) \bigg|_{\pi/6}^0$$
$$\therefore A = \frac{\pi}{6}$$
Anthonysrc
- answered
- 1841 views
- $2.13
Related Questions
- Find $\int \sec^2 x \tan x dx$
- Existence of a Divergent Subsequence to Infinity in Unbounded Sequences
- Find equation of the tangent line using implicit differentiation
- Show that the MLE for $\sum_{i=1}^{n}\left(\ln{2x_i} - 2\ln{\lambda} - \left(\frac{x_i}{\lambda}\right)^2\right)$ is $\hat{\lambda} = \sqrt{\sum_{i=1}^{n}\frac{x_i^2}{n}}$.
- Does an inequality of infinite sums imply another?
- Evluate $\int_{|z|=3}\frac{1}{z^5(z^2+z+1)}\ dz$
- Find the equation of the tangent line through the function f(x)=3x$e^{5x-5} $ at the point on the curve where x=1
- Calculus helped needed asap !!
