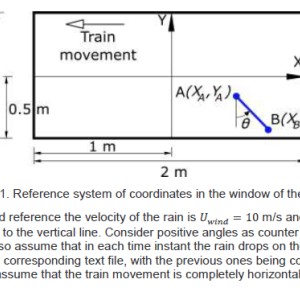
Obtaining the absolute velocity of a moving train based on angle of raindrops with respect to vertical axis
The problem is in the files attached.
I have been given the coordinates of the raindrops both start and end.
My question is how do I obtain the angle, and after that how do I arrange the equation to get Vtrain.
 Ice578
Ice578
Answer
- The questioner was satisfied with and accepted the answer, or
- The answer was evaluated as being 100% correct by the judge.
-
Leave a comment if you need any clarifications.
-
Thank you Philip, is ThetaWind always 30 degrees? I still dont quite get how to obtain the angle from the coordinates I was given. However everything you explained makes sense now.
-
In general ThetaWind may not be 30 degrees, but in your problem it is assumed to be 30 degrees.
-
Oh okay, so if I understand the assignment the first step in finding Vtrain should be to find the angle of the raindrop vectors using the coordinates that I was given? Should I do that using the slope?
-
Yes.
-
Great, thank you for the help Philip :),
-
Sorry for asking again Philip, but how would I obtain Vtrain with respect to a fixed refrence, so the absolute velocity of the train?
- answered
- 1679 views
- $4.92
Related Questions
- A question about the mathematical constant e.
- Epsilon-delta definitoon of continuity for $f : x → x^3$
- Convergence integrals
- Find $\lim _{x \rightarrow 0} x^{x}$
- Given $|f(x) - f(y)| \leq M|x-y|^2$ , prove that f is constant.
- Solving for two unknown angles, from two equations.
- Help with Business calculus. Finding derivative for X of given function.
- Connected rates of change calculus.