Discete Math

1) Let G be the graph whose vertices are all permutations of the integers of the set {1,2,…,10} with the property that two vertices (ε1,ε2,…,ε10) , (ε′1,ε′2, ...,ε′10) are connected by an edge if one vertex arises from the other by exchanging the positions of two integers εi,εj with εi,εj≤5
For example the vertices (1,2,7,4,8,5,3,10,9,6), (1,5,7,4,8,2,3,10,9,6) form an edge, vertices (1,2,4,8,10,7,3,5,9,6), (1,10,4,8,2,7,3,5,9,6) do not form an edge, vertices (1,7,2,4,8,10,3,5,9,6) , (1,10,2,4,8,7,3,5,9,6) do not form an edge. Find the number of edges of the graph G

2)How many induced subgraphs with 4 vertices does the complete graph K10 have? (We consider the vertices of K10 distinguished, i.e. named from 1 to 10)

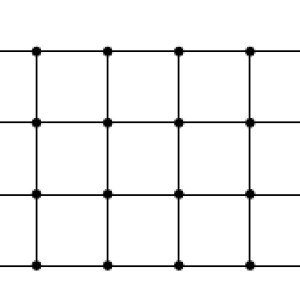
3) The graph in the figure below is bipartite. Right or wrong?